16. 基于时间的反向传播算法 (第一部分)
现在我们已经充分了解如何训练循环神经网络。
我们训练循环神经网络时,也使用反向传播算法,不过概念上发生了变化。这个过程与前馈神经网络(FFNN)类似,不过我们需要考虑以前的时间步长,因为系统包括存储。这个过程称为基于时间的反向传播算法,是接下来三个视频的主题。
- 与之前一样,不要忘记做笔记。
19 循环神经网络:基于时间的反向传播算法 A V6 最后一节
在深入分析基于时间的反向传播算法前,我们需要提醒一下。
状态向量\bar{s}_t通过以下方式计算:
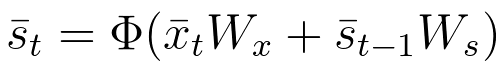
方程式33
输出向量\bar{y}_t是状态向量\bar{s}_t和矩阵W_y对应要素的乘积。如前所述,如果理想的输出在 0 和 1 之间,我们也可以使用 softmax 函数。以下方程组描述了这些计算:
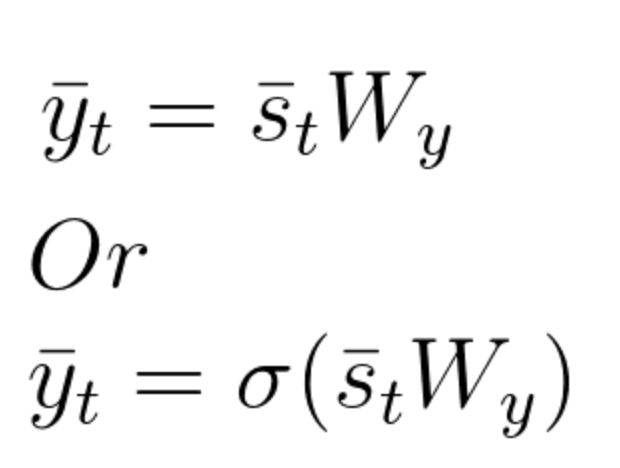
方程式 34
如前所述,对于误差计算,我们会使用损失函数,其中
E_t表示时间 t 的输出误差
d_t表示时间 t 的理想输出
y_t表示在时间 t 的计算输出
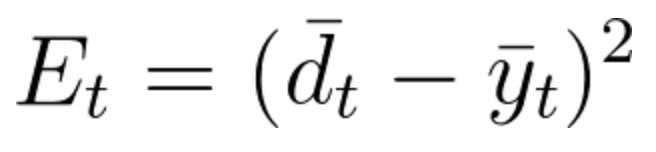
方程式35
在 基于时间的反向传播算法 (BPTT)中,我们在时间步长 t 训练网络,也会考虑之前的所有步长。
解释这个理论最简单的方法是直接进入示例讲解。
在这个例子中,我们将关注时间步长 t=3 时基于时间的反向传播算法过程。你会发现为了调整所有三个权重矩阵W_x, W_s 和 W_y ,我们需要考虑时间步长3、时间步长2和时间步长1。
我们关注时间步长 t=3 时,损失函数为E_3=(\bar{d}_3-\bar{y}_3)^2
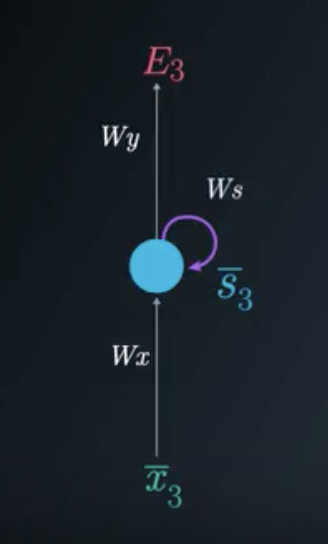
时间步长 3 的折叠模型
为了更新每个权重矩阵,我们需要找到时间为 3 损失函数的偏导数,作为所有权重矩阵的函数。我们将使用梯度下降,修改每个矩阵,同时考虑之前的时间步长。
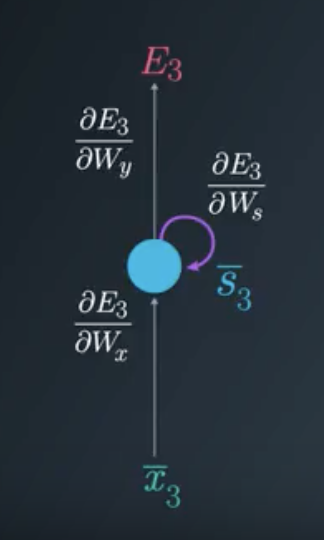
折叠模型中的梯度